Discussion of Similarity Metrics

Pearson Correlation Coefficient

Analysis

Unlike the Euclidean Distance similarity score (which is scaled from 0 to 1), this metric measures how highly correlated are two variables and is measured from -1 to +1. Similar to the modified Euclidean Distance, a Pearson Correlation Coefficient of 1 indicates that the data objects are perfectly correlated but in this case, a score of -1 means that the data objects are not correlated. In other words, the Pearson Correlation score quantifies how well two data objects fit a line.

There are several benefits to using this type of metric. The first is that the accuracy of the score increases when data is not normalized. As a result, this metric can be used when quantities (i.e. scores) varies. Another benefit is that the Pearson Correlation score can correct for any scaling within an attribute, while the final score is still being tabulated. Thus, objects that describe the same data but use different values can still be used. Figure 1 demonstrates how the Pearson Correlation score may appear if graphed.

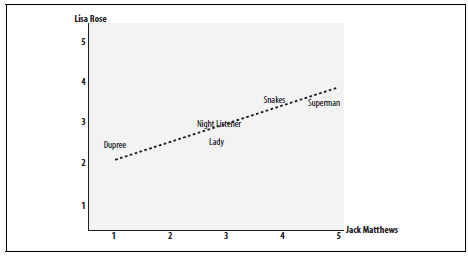
Figure 1. A chart demonstates the Pearson Correlation Coefficient. The axes are the scores given by the labeled critics and the similarity of the scores given by both critics in regards to certain an_items.

In essence, the Pearson Correlation score finds the ratio between the covariance and the standard deviation of both objects. In the mathematical form, the score can be described as:


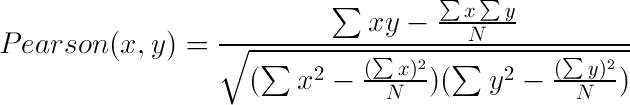
In this equation, (x,y) refers to the data objects and N is the total number of attributes

Python Implementation

# Input: 2 objects
# Output: Pearson Correlation Score
def pearson_correlation(object1, object2):
    values = range(len(object1))
    
    # Summation over all attributes for both objects
    sum_object1 = sum([float(object1[i]) for i in values]) 
    sum_object2 = sum([float(object2[i]) for i in values])

    # Sum the squares
    square_sum1 = sum([pow(object1[i],2) for i in values])
    square_sum2 = sum([pow(object2[i],2) for i in values])

    # Add up the products
    product = sum([object1[i]*object2[i] for i in values])

    #Calculate Pearson Correlation score
    numerator = product - (sum_object1*sum_object2/len(object1))
    denominator = ((square_sum1 - pow(sum_object1,2)/len(object1)) * (square_sum2 - 
    	pow(sum_object2,2)/len(object1))) ** 0.5
        
    # Can"t have division by 0
    if denominator == 0:
        return 0

    result = numerator/denominator
    return result
  

References

The previous content is based on Chapter 2 of the following book:
Segaran, Toby. Programming Collective Intelligence: Building Smart Web 2.0 Applications. Sebastopol, CA: O'Reilly Media, 2007.

Next: Tanimoto Coefficient
Back to: Euclidean Distance