Clustering Algorithms

Hierarchial Clustering

The Algorithm

As previously mentioned, hierarchial clustering involves grouping the two closest clusters until only one cluster remains. The distance between clusters is determined by their similarity. This process is better demonstrated with the following figure.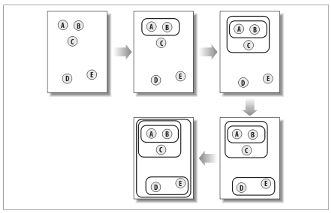
Figure 1. Objects being clustered hierarchically.

As seen with the figure above, each element is initially considered to be separate clusters. After each iteration, the closest elements are clustered together and this process repeats until a single cluster contains all the elements in the dataset. It is important to note that each cluster represents one of two possibilities:

1. A point in the tree with 2 branches
2. An endpoint that relates a row from the dataset

While hierarchical clustering is effective at showing how different pieces of data varies from other data, this form of clustering has its disadvantages. The primary disadvantage is that hierarchical clustering is only effective at splitting data small amounts of data. When the data set is small, patterns and relationships between clusters are easily discernable. As the data grows, so does the dendrogram and this usually results in the loss of information.

Visualizing the data

Since viewing the clusters after each iteration is inefficient, a dendrogram is used to visualize how each cluster was grouped (and therefore, the distance between clusters). Based on figure 1 (above), the following dendrogram is created.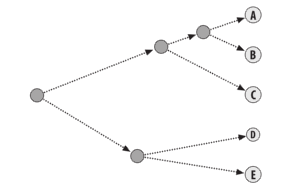
Figure 2. A dendrogram used to visualize data from Figure 1

Python Implementation

# Create class to represent the hierarchical clustering algorithm
# Each cluster is: 1. A point in the tree w/2 branches or 2. Endpoint associated w/ row from data
# Clusters have data about location (either row data for endpts or merged data from its 2 branches)
class tree:
  def __init__(self,data_list,left_subtree=None,right_subtree=None,distance=0.0,id=None):
    self.left_subtree=left_subtree
    self.right_subtree=right_subtree
    self.data_list=data_list
    self.id=id
    self.distance=distance


# Hierarchical clustering algorithm:
#   1. Create group of clusters containing original items
#   2. Find 2 objects that are the closest together (ie iterate through
#      all items and find Pearson correlation) and merge.
#      Data = avg(2 objects)
#   3. Repeat until 1 cluster left w/ all objects
#
# Store correlation in array, since it's calculated repeatedly w/ the
#   same objects (@ least when individual objects are clusters)
def hierarchical_cluster(rows,distance=pearson_correlation):
  distance_cache={}
  current_cluster_id=-1

   # Performing step 1 of algorithm
  cluster   = [tree(rows[i],id=i) for i in range(len(rows))]

  while len(cluster)>1:
    lowest_pair=(0,1)
    closest=distance(cluster[0].data_list,cluster[1].data_list)

		# Performing step 2 of algorithm
       # loop through every pair looking for the smallest distance
    for i in range(len(cluster)):
      for j in range(i+1,len(cluster)):
        # Check the distance_cache dict for any previously calculated distances
       	if (cluster[i].id,cluster[j].id) not in distance_cache: 
          distance_cache[(cluster[i].id,cluster[j].id)]=distance(cluster[i].data_list,cluster[j].data_list)

        closer_distance=distance_cache[(cluster[i].id,cluster[j].id)]

        if closer_distance<closest:
          closest=closer_distance
          lowest_pair=(i,j)

    # Nearing the end of step 2- find the avg b/w closest pair
    merge_clusters=[
    (cluster[lowest_pair[0]].data_list[i]+cluster[lowest_pair[1]].data_list[i])/2.0 
    for i in range(len(cluster[0].data_list))]

    # create the new cluster
    new_cluster=tree(merge_clusters,left_subtree=cluster[lowest_pair[0]],
                         right_subtree=cluster[lowest_pair[1]],
                         distance=closest,id=current_cluster_id)

    # Cluster ids that are not in the original set are negative
    current_cluster_id-=1
    del cluster[lowest_pair[1]]
    del cluster[lowest_pair[0]]
    cluster.append(new_cluster)

  return cluster[0]

  

References

The previous content is based on Chapter 3 of the following book:
Segaran, Toby. Programming Collective Intelligence: Building Smart Web 2.0 Applications. Sebastopol, CA: O'Reilly Media, 2007.

Next: K-Means Clustering
Back to: Clustering Algorithms Index