Bayesian Classifier
In essence, the Bayesian classifier turns a given dataset into a list of features - either the presence or absence for each item in the dataset. An example of supervised classifer, this type of classifier relies on being trained via example before being able to classify unlabeled datasets.
During training, the Bayesian classifier tracks all features that it has been trained on and calculates the probability of features being associated with a specific classification. Since this classifier can only train on example one at a time, the probabilities are updated at the end of each training example. Ideally, the end result should be a classifier that contains all the probabilities in order to label the test dataset perfectly.
An advantage that the Bayesian classifier has over other types of classifiers is that this classifier only needs its list of probabilities, not the training data. This adds value, in terms of memory and computation efficiency. Also, it is fairly simple to determine what the classifier has learned at any given point in time. On the other hand, this classifier relies on the class labels (for the features) being distinct and unique. As a result, the classifier is not able to handle combinations of features.
As mentioned before, the focal point of Bayesian classifier is the probabilities, specifically Bayes' Theorem. In words, this theorem states that the probability of an item occuring given another item is equal to the probability of the second item occuring given that first item occurs, multiplied by the probability of the first item occuring, regardless. This product is divided by the probability of the second item occuring. Mathematically, Bayes' Theorem is provided below.
A = the first item
B = the second item
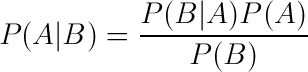
Figure 1. The mathematical representation of Bayes' Theorem.
# Python Implementation of the Bayesian Classifier
import re
import math
from pysqlite2 import dbapi2 as sqlite
# break text into words by dividing text on any character not a letter
# convert to lowercase
def getwords(doc):
splitter = re.compile('\\W*')
# split words by non-alphabetical characters
words = [s.lower() for s in splitter.split(doc) if len(s)>2 and len(s)<20]
# return unique set of words
return dict([(w, 1) for w in words])
# dumped some training data into the classifier to do this automatically
def sampletrain(cl):
cl.train('Nobody owns the water.','good')
cl.train('the quick rabbit jumps fences','good')
cl.train('buy pharmaceuticals now','bad')
cl.train('make quick money at the online casino','bad')
cl.train('the quick brown fox jumps','good')
# classifier will learn how to classify a document via training
# designed to start off very uncertain & increase in certainty as it learns which features are important
class classifier:
def __init__(self, getfeatures, filename=None):
# counts of feature/category combinations
# includes count of how many times a word is used as spam or in an actual document
# ie {some word: {bad:0, good:6}, another word: {bad:3, good:3}}
self.fc ={}
# counts of documents in each category
# dictionary of how many times every classification has been used
self.cc = {}
# extract features from items being classified (getwords)
self.getfeatures = getfeatures
# set up SQLite to persist training info for classifier
def setdb(self, dbfile):
self.con = sqlite.connect(dbfile)
self.con.execute('create table if not exists fc(feature, category, count)')
self.con.execute('create table if not exists cc(category, count)')
# Increase the count of a feature/category pair
def incf(self, f, cat):
count = self.fcount(f, cat)
if count == 0:
self.con.execute("insert into fc values('%s','%s',1)" % (f, cat))
else:
self.con.execute("update fc set count=%d where feature= '%s' and category='%s'" % (count+1, f, cat))
# increase count of a category
def incc (self, cat):
count = self.catcount(cat)
if count == 0:
self.con.execute("insert into cc values ('%s',1)" % (cat))
else:
self.con.execute("update cc set count=%d where category='%s'" % (count+1, cat))
# #of times a feature has appeared in category
def fcount (self, f, cat):
res = self.con.execute('select count from fc where feature="%s" and category="%s"' % (f, cat)).fetchone()
if res == None:
return 0
else:
return float(res[0])
# # of items in category
def catcount(self, cat):
res = self.con.execute('select count from cc where category = "%s"' % (cat)).fetchone()
if res == None:
return 0
else: return float(res[0])
# total # of items
def totalcount(self):
res = self.con.execute('select sum(count) from cc').fetchone()
if res == None:
return 0
return res[0]
# list of all categories
def categories(self):
cur = self.con.execute('select category from cc')
return [d[0] for d in cur]
# take item & classification. use getfeatures to break item into separate features
# call incf to increase count for the classification for every feature
# increase total count for classification
def train(self, item, cat):
features= self.getfeatures(item)
self.con.commit()
# increment the count for every feature w/ the category
for f in features:
self.incf(f, cat)
# increment count for category
self.incc(cat)
# calculate the probability that a word is in a particular category: P = ( # of times word is in document / # of documents ) in a category
def fprob(self, f, cat):
if self.catcount(cat) == 0:
return 0
# return the probability
return self.fcount(f, cat)/self.catcount(cat)
# use weighted probability to decrease the initial sensitivity to training data
# start with an assumed probability = 0.5 before training data changes the actual weight
def weightedprob(self, f, cat, prf, weight=1.0, ap=0.5):
# Find current probability
basicprob = prf(f, cat)
# count # of times word(f) appears in all categories
totals = sum([self.fcount(f, c) for c in self.categories()])
# calculate weighted average
bp = ((weight*ap)+(totals*basicprob))/(weight+totals)
return bp
# Naive Bayesian classifier
class naivebayes(classifier):
# first must find probability of entire document being given a classification
# assume all probabilities are independent (probability = multiply(all probabilities))
def docprob(self, item, cat):
features = self.getfeatures(item)
# multiply probabilities of all features together
p=1
for f in features:
p *= self.weightedprob(f, cat, self.fprob)
return p
# calculate probability using Bayes' theorem
def prob(self, item, cat):
catprob = self.catcount(cat)/self.totalcount()
docprob = self.docprob(item, cat)
return docprob*catprob
# set up min threshold for each category
# this allows new item to be classified into particular category, probability should be greater than the threshold for other categories
def __init__(self, getfeatures):
classifier.__init__(self, getfeatures)
self.thresholds = {}
# get & set threshold
def setthreshold(self, cat, t):
self.thresholds[cat] = t
def getthreshold(self, cat):
if cat not in self.thresholds:
return 1.0
return self.thresholds[cat]
# calculate probability for each category & find largest & if largest - next largest > threshold
# if not possible, use default values
def classify (self, item, default=None):
probs = {}
# find category w/ highest probability
max = 0.0
for cat in self.categories():
probs[cat] = self.prob(item, cat)
if probs[cat] > max:
max = probs[cat]
best = cat
# ensure probability > threshold*next best
for cat in probs:
if cat == best: continue
if probs[cat] * self.getthreshold(best)>probs[best]:
return default
return best
# Fisher Method Alg
# 1. calculate probability of a category for each feature in document
# 2. combine probabilities & test if set of probabilities is more/less likely than random self
# 3. return probability for each category
# perform normalization of probabilities since there maybe many good documents & few bad, vice versa
# to find:
# 1. find P(feature|category) for 1 category
# 2. sum above probability for all categories
# 3. 1/(1+2)
class fisherclassifier(classifier):
def cprob(self, f, cat):
# frequency of feature in categories
clf = self.fprob(f, cat)
if clf == 0: return 0
# frequency of feature in all categories
freqsum = sum([self.fprob(f, c) for c in self.categories()])
# probability = frequency in this category / overall frequency
p = clf/(freqsum)
return p
# Fisher probability
# multiply all probabilities together, ln(product), result*-2
def fisherprob(self, item, cat):
# multiply all probabilities together
p=1
features = self.getfeatures(item)
for f in features:
p*=(self.weightedprob(f, cat, self.cprob))
# ln(product), result * -2
fscore = -2*math.log(p)
# use inverse chi2 func to get probability
# if probabilities are independent & random, result would fit a chi-squared distribution
return self.invchi2(fscore, len(features)*2)
def invchi2(self, chi, df):
m = chi / 2.0
sum = term = math.exp(-m)
for i in range(1, df//2):
term *= m / i
sum += term
return min(sum, 1.0)
# specify lower bounds on each classification & classifier returns highest value w/i bounds
# set minimum high for bad classification & low for good classification
def __init__(self, getfeatures):
classifier.__init__(self, getfeatures)
self.minimums = {}
def setminimum(self, cat, min):
self.minimums[cat] = min
def getminimum(self, cat):
if cat not in self.minimums:
return 0
return self.minimums[cat]
# calc prob for each category & find best result exceeding minimum
def classify(self, item, default=None):
# loop & find best result
best = default
max = 0.0
for c in self.categories():
p = self.fisherprob(item, c)
# ensure exceeds min
if p > self.getminimum(c) and p > max:
best = c
max = p
return best
References
The previous content is based on Chapter 6 of the following book:Segaran, Toby. Programming Collective Intelligence: Building Smart Web 2.0 Applications. Sebastopol, CA: O'Reilly Media, 2007.