Discussion of Similarity Metrics

Cosine Similarity

Analysis

This metric is frequently used when trying to determine similarity between two documents. Since there are more words that are incommon between two documents, it is useless to use the other methods of calculating similarities (namely the Euclidean Distance and the Pearson Correlation Coefficient discussed earlier). As a result, the likelihood that two documents do not share the majority is very high (as with the Tanimoto Coefficient) and does not create a satisfactory metric for determining similarities.

In this similarity metric, the attributes (or words, in the case of the documents) is used as a vector to find the normalized dot product of the two documents. By determining the cosine similarity, the user is effectively trying to find cosine of the angle between the two objects. For cosine similarities resulting in a value of 0, the documents do not share any attributes (or words) because the angle between the objects is 90 degrees.

Expressed as a mathematical equation:

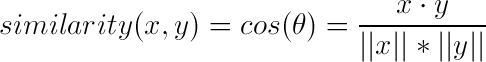
Python Implementation

# Input: 2 vectors
# Output: the cosine similarity
# !!! Untested !!!
def cosine_similarity(vector1,vector2):
  # Calculate numerator of cosine similarity
  dot = [vector1[i] * vector2[i] for i in range(vector1)]
  
  # Normalize the first vector
  sum_vector1 = 0.0
  sum_vector1 += sum_vector1 + (vector1[i]*vector1[i] for i in range(vector1))
  norm_vector1 = sqrt(sum_vector1)
  
  # Normalize the second vector
  sum_vector2 = 0.0
  sum_vector2 += sum_vector2 + (vector2[i]*vector2[i] for i in range(vector2))
  norm_vector2 = sqrt(sum_vector2)
  
  return (dot/(norm_vector1*norm_vector2))
  

References

The previous content is based on Chapter 2 of the following book:
Tan, Pang-Ning, Michael Steinbach, and Vipin Kumar. Introduction to Data Mining. Boston: Pearson Addison Wesley, 2006.

Next: Similarity Index
Back to: Tanimoto Coefficient