Data Mining Portfolio

Measures of Similarity in Data

This page is a quick overview of each of the similarity metrics we examined in the course. For algorithms we implemented, sample source code is provided.

What is a similarity metric?

A simple - and slightly circular - definition of similarity is a numerical measure of the degree to which two data objects are alike.¹ The definition of what makes two pieces of data "alike" can vary depending on what the data represents and the attributes. In general, two objects are similar if they share many categorical attributes, or if the values of their numerical attributes are relatively close. Often, categorical attributes must be transformed into binary attributes indicating whether or not the data object belongs to that category. Regardless of the measure of similarity used, a high similarity score indicates that two data objects are closely related. The opposite of similarity is, unsurprisingly, dissimilarity, which is often referred to as the distance between two objects.

Similarity roughly falls into one of two classes:

Minkowski distance
Similarity coefficients

Minkowski distance

Minkowski distance refers to a family of measures related by the formula²:

The astute reader might notice that when p=2, the Minkowski distance formula is simply the formula for Euclidean distance - the same formula from high school geometry class. To visualize the Euclidean distance similarity between two objects, imagine that each is plotted in an n-dimensional space. Their similarity is the straight line distance between the points.

Here is a simple Python implementation of the Euclidean distance algorithm used to calculate the similarity between two people based on their ratings of movies. It is adapted from [3]

# Calculate the Euclidean distance between two critics
# @param prefs Multi-dimensional dictionary containing preferences for each critic
# @param person1 Name of a person in the prefs dict
# @param person2 Name of a another person in the prefs dict
def euclidean_distance(prefs, person1, person2) :
	#Shared items will store all the movies that both have watched
	shared_items = {}
	for movie in prefs[person1]:
		if movie in prefs[person2]:
			shared_items[movie] = 1

	# If they haven't seen any of the same movies, return 0
	if len(shared_items) == 0:
		return 0

	# Add the squares of all the distances, which is the 
	# first step in the Euclidean distance formula
	sum_of_squares = sum( [pow(prefs[person1][movie] - prefs[person2][movie], 2) for movie in shared_items])

	return 1/(1+sqrt(sum_of_squares))

When p=1, the Minkowski formula reduces to the common Manhattan distance, which can be used to measure, for example, the number of bits that differ between two binary vectors.

Minkowski distances are really only useful for data comprised of numerical attributes. For market basket-type data composed of a large number of binary attributes, Minkowski distances have little use because the distance will go to 0 for sparse data sets.

Similarity coefficients

For data with non-numerical attributes, it is often useful to transform categorical attributes into binary attributes. Since Minkowski distances don't handle binary data well, another class of similarity metrics is often used, similarity coefficients.

Simple Matching Coefficient

The simplest similarity coefficient is called the Simple Matching Coefficient, which is defined by the following formula^[3]:

where:
f₀₀ = number of attributes where x is 0 and y is 0
f₀₁ = number of attributes where x is 0 and y is 1
f₁₀ = number of attributes where x is 1 and y is 0
f₁₁ = number of attributes where x is 1 and y is 1

In many cases, the SMC is inadequate because it treats 0 and 1 as equally important. Often, we are only concerned about when both objects have a 1 for a particular attribute.

Jaccard Coefficient

The Jaccard coefficient handles asymmetric binary data by only counting the number of times the two objects share a 1 for an attribute. This is particularly useful for sparse data like the classic market basket data sets, where the large majority of attributes will be 0. Jaccard is defined with the formula:

Cosine Similarity

In some cases, it is desirable to ignore 00 matches, but also account for matches with more than one occurance. For example, when comparing the document vector of two texts, it is useful to factor in the number of times a particular word appears in both texts. In this case, it is useful to use the cosine similarity, which is defined as the dot product of the two vectors over the product of their magnitudes:

Similar to Jaccard, cosine similarity can be used to measure asymmetric binary data, though they the two measures won't produce the same result. Cosine similarity can be adapted to reduce to the Jaccard coefficient in the case of binary data. This is called the Tanimoto coefficient, or extended Jaccard coefficient, and is defined as:

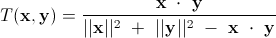
Here is a general Python implementation of the Tanimoto coefficient:

# Calculate the tanimoto coefficient for two values
# param @value1 First data object to compare
# param @value2 Second data object to compare
def tanimoto(value1, value2):
	# The tanimoto coefficent depends on how many items
	# the two objects share. These variables keep count
	count1, count2, shared = 0, 0, 0
	
	for i in range(len(value1)):
		if value1[i] != 0: 
			count1+=1
		if value2[i] != 0: 
			count2+=1
		if value1[i] != 0 and value2[i] != 0:
			shared += 1
	return 1.0 - (float(shared)/(count1+count2-shared))

It is worth noting that Jaccard is often more efficient to compute because it doesn't need to calculate the dot product of the vectors.

Pearson Correlation Coefficient

Sometimes data is not well normalized because of a systematic bias. The metrics examined so far cannot handle non-normalized data, so we introduce the Pearson Correlation Coefficient. Pearson is a measure of the linear relationship between attributes of a pair of objects. That is, how closely do the attribute pairs come to fitting on a straignt line. The formula is:

Here is a Python implementation of the Pearson correlation coefficient:

# Calculate the pearson correlation coefficient
def pearson( value1, value2 ):
	# Check that value1 and value2 have the same length
	# Explode otherwise
	if len(value1) != len(value2):
		print "The two values weren't the same length!"
		print len(value1)
		print len(value2)
		return None	

	# Simple sums
	sum1 = sum(value1)
	sum2 = sum(value2)
	
	# Sum the squares of the values
	sum1squares = sum([pow(v,2) for v in value1])
	sum2squares = sum([pow(v,2) for v in value2])

	# Sum of the products (to be used in calculating covariance)
	productSum = sum([value1[i]*value2[i] for i in range(len(value1))])
	
	# Calculate r (The pearson correlation coefficient)
	numerator = productSum-(sum1*sum2/len(value1))
	denominator = sqrt((sum1squares-pow(sum1,2)/len(value1))*(sum2squares-pow(sum2,2)/len(value2)))
	if denominator == 0:
		return 0
	
	return 1.0-numerator/denominator

References

Tan, Pang-Ning, Michael Steinbach, and Vipin Kumar. Introduction to Data Mining. Boston: Pearson Addison Wesley, 2006. Print.
http://en.wikipedia.org/wiki/Minkowski_distance
Segaran, Toby. Programming Collective Intelligence: Building Smart Web 2.0 Applications. Beijing: O'Reilly, 2007. Print.

Seth Daugherty