Mining Similarity Using Euclidean Distance, Pearson Correlation, and Filtering

How do we express similarity in a machine?

There are many ways to determine the similarity between two things. In order to represent this similarity in a machine, we need to define a similarity score. If we can quantify different attributes of data objects, we can employ different similarity algorithms across those attributes that will yield similarity scores between the different data objects. For example, we can represent people as data objects whose attributes are tastes in movies. We can use a similarity metric to help us find which people are similar based on how similar their tastes in movies are. We just need to quantify the attribute of movie tastes; for instance, we could use those people's numerical movie ratings. Now we can use one of similarity metrics discussed below to produce similarity scores.

Euclidean Distance

A simple yet powerful way to determine similarity is to calculate the Euclidean Distance between two data objects. To do this, we need the data objects to have numerical attributes. We also may need to normalize the attributes. For example, if we were comparing people's rankings of movies, we need to make sure that the ranking scale is the same across all people; it would be problematic to compare someone's rank of 5 on a 1-5 scale and another person's 5 on a 1-10 scale. The next step is to apply the Euclidean distance formula: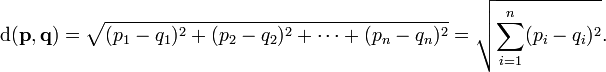



We subtract each attribute in one data object from the other corresponding attribute and add them in quadrature. The result is the "distance" between the two data objects. The shorter the distance, the more similar the data objects are.

Pearson Coefficient

The Pearson Coefficient is a more complex and sophisticated approach to finding similarity. The method generates a "best fit" line between attributes in two data objects.



A line that runs through all the data points and has a positive slope represents a perfect correlation between the two objects. This best fit line is generated by the Pearson Coefficient which is the similarity score. The Pearson Coefficient is found using the following equation: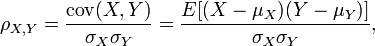



The coefficient is found from dividing the covariance by the product of the standard deviations of the attributes of two data objects. The advantage of the Pearson Coefficient over the Euclidean Distance is that it is more robust against data that isn't normalized. For example, if one person ranked movies "a", "b", and "c" with scores of 1, 2, and 3 respectively, he would have a perfect correlation to someone who ranked the same movies with a 4, 5, and 6.

Jaccard Coefficient

When dealing with data objects that have binary attributes, it is more effective to calculate similarity using a Jaccard Coefficient. The equation to find the Jaccard Coefficient is as follows:



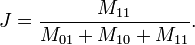
The M11 represents the total number of attributes where both data objects have a 1. The M10 and M01 represent the total number of attributes where one data object has a 1 and the other has a 0. The total matching attributes are then divided by the total non-matching attributes plus the matching ones. A perfect similarity score would then be a 1. For example, if object "A" had attributes of 1, 0, 1, and object "B" had attributes of 1, 1, 1, the Jaccard Coefficient would be 2/3. This method eliminates matching attributes that share a 0, which makes it great for sparse data sets, or ones where most of the attributes are 0's. For instance, if one were to record purchases in a grocery store by having a 1 for each item purchased and a 0 for items not purchased by a particular customer, the customer would have a lot of 0's and only a few 1's if the whole inventory of the store was taken into account. So when one customer is compared to another, all those items that weren't purchased by either person are not factored into the Jaccard Coefficient when finding how similar the people are.

Cosine Similarity

Finding the cosine similarity between two data objects requires that both objects represent their attributes in a vector. Similarity is then measured as the angle between the two vectors.



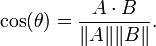
This method is useful when finding the similarity between two text documents whose attributes are word frequencies. A perfect correlation will have a score of 1 (or an angle of 0) and no correlation will have a score of 0 (or an angle of 90 degrees).

Tanimoto Coefficient

The Tanimoto coefficient is an extended version of the Jaccard Coefficient and cosine similarity. It also assumes that each data object is a vector of attributes. The attributes may or may not be binary in this case. If they all are binary, the Tanimoto method reduces to the Jaccard method. The Tanimoto Coefficient is found from the following equation: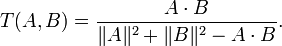



In the equation, A and B are data objects represented by vectors. The similarity score is the dot product of A and B divided by the squared magnitudes of A and B minus the dot product. Using the grocery store example, the Tanimoto Coefficient ensures that a customer who buys five apples and one orange will be different from a customer who buys five oranges and an apple.

Euclidean Implementation

The following code is the python implementation of the Euclidean Distance similarity metric. The code was written to find the similarities between people based off of their movie preferences. The preferences contain the ranks (from 1-5) for numerous movies. The returned score was normalized to be between 0 and 1. A shorter distance (more similarity) gave a score closer to 1 while a longer distance (less similarity) gave a score closer to 0.

  #Return a Euclidean Distance similarity score for person1 and person2
  def euclidean_distance(preferences, person1, person2):

    #Get the list of shared items
    shared_items = {}
    for item in preferences[person1]:
    	if item in preferences[person2]:
        	shared_items[item]=1
            
    #If they have no ratings in common, return 0
    if len(shared_items)==0: return 0
    
    #Add up the squares of all the differences
    sum_of_squares = sum([pow(preferences[person1][item]-preferences[person2][item],2)
                          for item in preferences[person1] if item in preferences[person2]])
    
    return 1/(1+sqrt(sum_of_squares))
  

Pearson Implementation

The following python code implements the Pearson Coefficient for the same data described above.

  #Return the Pearson Coefficient for person1 and person2
  def similarity_pearson(preferences, person1, person2):
  
    #Get the list of mutually rated items
    shared_items={}
    for item in preferences[person1]:
        if item in preferences[person2]: shared_items[item]=1
        
    #Find the number of elements
    num_shared = len(shared_items)
    
    #If there are no ratings in common, return 0
    if num_shared == 0: return 0
    
    #Add up all the preferences
    sum1 = sum([preferences[person1][item] for item in shared_items])
    sum2 = sum([preferences[person2][item] for item in shared_items])
    
    #Sum up the squares
    sum1_squares = sum([pow(preferences[person1][item],2) for item in shared_items])
    sum2_squares = sum([pow(preferences[person2][item],2) for item in shared_items])
    
    #Sum up the products
    prod_sum = sum([preferences[person1][item]*preferences[person2][item] for item in shared_items])
    
    #Calculate the Pearson score
    num = prod_sum - (sum1*sum2/num_shared)
    den = sqrt((sum1_squares-pow(sum1,2)/num_shared)*(sum2_squares - pow(sum2,2)/num_shared))
    if den == 0: return 0
    r = num/den
    
    return r
  

NOTE: The python code was obtained from the book Collective Intelligence written by Toby Segaran. The images/equations were pulled from Wikipedia.