Data Mining and Classifiers:
What are classifiers?
A classification algorithm is one that builds a model that can take in data objects and assign them class labels depending on the object's attributes. Simply put, the algorithm classifies data according to its properties. In order to do that, classifiers need to be built from a sampling of a data set, also known as a training set. Once the classifier is trained, it can then predict how data should be classified. Practically speaking, classifiers are used in things such as spam filters or taxonomy problems. Additionally, classifiers are behind powerful search engines such as Google in predicting desired search results.
ANNs:
An ANN, or Artificial Neural Network is a type of classifier that immitates a biological neural network, such as a brain.
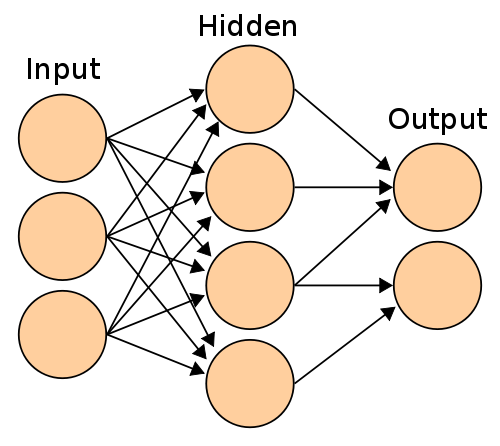
This classifier consists of nodes that apply an activation function when certain conditions are met when a set of training data . The outputs are then compared to what they should actually be, and the error is factored into adjusting the condition criteria that future inputs need to meet. The same set of inputs are then passed into the now adjusted ANN and the process repeats. The procedure makes the ANN more and more accurate after each iteration. When unknown data is then passed in, the ANN can either predict a classification or learn from the new inputs.
The following code is an implementation of an ANN coded in Python for a search engine:
# This class will contain the meat of the neural network. It will connect and initiate a database for the hidden
# layer and connections to the database of words and urls. The neural network will be a self learning mechanism
# that will score pages based on how many times they are visited
class searchnet:
# This function will open a connection to the database
def __init__(self,dbname):
self.con=sqlite.connect(dbname)
# This function closes the connection to the database
def __del__(self):
self.con.close()
# This function will create the tables used for the hidden node as well as the connections between
# words and urls
def maketables(self):
self.con.execute('create table hiddennode(create_key)')
self.con.execute('create table wordhidden(fromid,toid,strength)')
self.con.execute('create table hiddenurl(fromid,toid,strength)')
self.con.commit()
# This function determines the strength of a connection. It will return a default value of -0.2 for
# links from words to the hidden layer and 0 for links from the hidden layer to urls.
def getstrength(self,fromid,toid,layer):
if layer==0: table='wordhidden'
else: table='hiddenurl'
res=self.con.execute('select strength from %s where fromid=%d and toid=%d' % (table,fromid,toid)).fetchone()
if res==None:
if layer==0: return -0.2
if layer==1: return 0
return res[0]
# This function determines if a connection exists and creates/updates a connection with a new strength
def setstrength(self,fromid,toid,layer,strength):
if layer==0: table='wordhidden'
else: table='hiddenurl'
res=self.con.execute('select rowid from %s where fromid=%d and toid=%d' % (table,fromid,toid)).fetchone()
if res==None:
self.con.execute('insert into %s (fromid,toid,strength) values (%d,%d,%f)' % (table,fromid,toid,strength))
else:
rowid=res[0]
self.con.execute('update %s set strength=%f where rowid=%d' % (table,strength,rowid))
# This function creates a new node in the hidden layer when it sees a new combination of words. It creates
# default weighted links between words and the hidden node as well as between the query node and the url
# results returned by the query
def generatehiddennode(self,wordids,urls):
if len(wordids)>3: return None
# Check if we already created a node for this set of words
sorted_words=[str(id) for id in wordids]
sorted_words.sort()
createkey='_'.join(sorted_words)
res=self.con.execute(
"select rowid from hiddennode where create_key='%s'" % createkey).fetchone()
# If not, create it
if res==None:
cur=self.con.execute(
"insert into hiddennode (create_key) values ('%s')" % createkey)
hiddenid=cur.lastrowid
# Put in some default weights
for wordid in wordids:
self.setstrength(wordid,hiddenid,0,1.0/len(wordids))
for urlid in urls:
self.setstrength(hiddenid,urlid,1,0.1)
self.con.commit()
# This function finds all the nodes from the hidden layer that are relevant to the specific query
def getallhiddenids(self,wordids,urlids):
l1={}
for wordid in wordids:
cur=self.con.execute(
'select toid from wordhidden where fromid=%d' % wordid)
for row in cur: l1[row[0]]=1
for urlid in urlids:
cur=self.con.execute(
'select fromid from hiddenurl where toid=%d' % urlid)
for row in cur: l1[row[0]]=1
return l1.keys()
# This function constructs the relevant network with all the current weights from the database.
def setupnetwork(self,wordids,urlids):
# value lists
self.wordids=wordids
self.hiddenids=self.getallhiddenids(wordids,urlids)
self.urlids=urlids
# node outputs
self.ai = [1.0]*len(self.wordids)
self.ah = [1.0]*len(self.hiddenids)
self.ao = [1.0]*len(self.urlids)
# create weights matrix
self.wi = [[self.getstrength(wordid,hiddenid,0)
for hiddenid in self.hiddenids]
for wordid in self.wordids]
self.wo = [[self.getstrength(hiddenid,urlid,1)
for urlid in self.urlids]
for hiddenid in self.hiddenids]
# This function takes in a list of inputs, pushes them through the network, and returns the output
# of all nodes in the output layer.
def feedforward(self):
# the only inputs are the query words
for i in range(len(self.wordids)):
self.ai[i] = 1.0
# hidden activations
for j in range(len(self.hiddenids)):
sum = 0.0
for i in range(len(self.wordids)):
sum = sum + self.ai[i] * self.wi[i][j]
self.ah[j] = tanh(sum)
# output activations
for k in range(len(self.urlids)):
sum = 0.0
for j in range(len(self.hiddenids)):
sum = sum + self.ah[j] * self.wo[j][k]
self.ao[k] = tanh(sum)
return self.ao[:]
# This function will set up the network and return the results of the feed forward algorithm
def getresult(self,wordids,urlids):
self.setupnetwork(wordids,urlids)
return self.feedforward()
#
def backPropagate(self, targets, N=0.5):
# this finds the difference or the error in the output
difference_in_output = [0.0] * len(self.urlids)
for k in range(len(self.urlids)):
error = targets[k]-self.ao[k]
difference_in_output[k] = dtanh(self.ao[k]) * error
# this finds the difference or the error in the hidden layer
difference_in_hidden_layer = [0.0] * len(self.hiddenids)
for j in range(len(self.hiddenids)):
error = 0.0
for k in range(len(self.urlids)):
error = error + difference_in_output[k]*self.wo[j][k]
difference_in_hidden_layer[j] = dtanh(self.ah[j]) * error
# this adjusts the output weights based upon the difference in the output
for j in range(len(self.hiddenids)):
for k in range(len(self.urlids)):
change_in_weight = difference_in_output[k]*self.ah[j]
self.wo[j][k] = self.wo[j][k] + N*change_in_weight
# this adjusts the weight of the inputs based on the difference in the hidden layer
for i in range(len(self.wordids)):
for j in range(len(self.hiddenids)):
change_in_weight = difference_in_hidden_layer[j]*self.ai[i]
self.wi[i][j] = self.wi[i][j] + N*change_in_weight
# This method takes in a list of word ids, url ids, and a selected url and then trains the network using
# the feed forward and back propagate methods
def trainquery(self,word_ids,url_ids,selected_url):
# generate a hidden node if necessary
self.generatehiddennode(word_ids,url_ids)
# Set up the neural network, use feed forward, and then backpropagate to determine
# new weights for each of the inputs and outputs
self.setupnetwork(word_ids,url_ids)
self.feedforward()
targets=[0.0]*len(url_ids)
targets[url_ids.index(selected_url)]=1.0
error = self.backPropagate(targets)
# Update the database
self.updatedatabase()
# This function updates the database with the new weights found from the training query
def updatedatabase(self):
# set them to database values
for i in range(len(self.wordids)):
for j in range(len(self.hiddenids)):
self.setstrength(self.wordids[i],self. hiddenids[j],0,self.wi[i][j])
for j in range(len(self.hiddenids)):
for k in range(len(self.urlids)):
self.setstrength(self.hiddenids[j],self.urlids[k],1,self.wo[j][k])
self.con.commit()
Bayesian Classifiers:
The premise of Bayesian Classifiers is that data is classified based off of probabilities. The classifier is built from a training set of numerical data. The training set creates a probability distribution for each class. When data is passed into the trained algorithm, it is tested against a threshold in each of the probability distributions and classified accordingly.
The following Python code is an implementation of a Bayesian Classifier for classifying text documents:
# This class uses a Bayesian approach to classifying entire documents. It employs methods to
# combine the probabilities of features to determine the probability of a bad or good document.
class naivebayes(classifier):
# Initialize the class to include category thresholds
def __init__(self,getfeatures):
classifier.__init__(self,getfeatures)
self.thresholds={}
# This function calculates the probability of a document based on a product of the features
def docprob(self,item,cat):
features=self.getfeatures(item)
# Multiply the probabilities of all the features together
p=1
for f in features: p*=self.weightedprob(f,cat,self.fprob)
return p
# This function calculates the probability of the category and returns a product of the
# document and category probabilities
def prob(self,item,cat):
catprob=self.catcount(cat)/self.totalcount()
docprob=self.docprob(item,cat)
return docprob*catprob
# This function sets the value of the thresholds
def setthreshold(self,cat,t):
self.thresholds[cat]=t
# This function gets the value of the thresholds and sets the value to 1 as a default
def getthreshold(self,cat):
if cat not in self.thresholds: return 1.0
return self.thresholds[cat]
# This function calculates the probability for each category and determines the largest
# and tests them against the threshold.
def classify(self,item,default=None):
probs={}
# Find the category with the highest probability
max=0.0
for cat in self.categories():
probs[cat]=self.prob(item,cat)
if probs[cat]>max:
max=probs[cat]
best=cat
# Make sure the probability exceeds threshold*next best
for cat in probs:
if cat==best: continue
if probs[cat]*self.getthreshold(best)>probs[best]: return default
return best
Decision Tree Classifiers:
A decision tree classifier will classify data based on nodes that split subsets of the data based on conditions. The algorithm begins by passing the whole data set to the beginning or root node, that node will split the records into branches based on the node condition. From there, additional levels of branches of the data are made from splits from additional nodes. The algorithm completes when all the data is placed into respective classes or a certain purity condition is met.
Below is an implementation of a decision tree written in Python:
class decisionnode:
def __init__(self,col=-1,value=None,results=None,tb=None,fb=None):
self.col=col
self.value=value
self.results=results
self.tb=tb
self.fb=fb
# Divides a set on a specific column. Can handle numeric
# or nominal values
def divideset(rows,column,value):
# Make a function that tells us if a row is in
# the first group (true) or the second group (false)
split_function=None
if isinstance(value,int) or isinstance(value,float):
split_function=lambda row:row[column]>=value
else:
split_function=lambda row:row[column]==value
# Divide the rows into two sets and return them
set1=[row for row in rows if split_function(row)]
set2=[row for row in rows if not split_function(row)]
return (set1,set2)
# Create counts of possible results (the last column of
# each row is the result)
def uniquecounts(rows):
results={}
for row in rows:
# The result is the last column
r=row[len(row)-1]
if r not in results: results[r]=0
results[r]+=1
return results
# Probability that a randomly placed item will
# be in the wrong category
def giniimpurity(rows):
total=len(rows)
counts=uniquecounts(rows)
imp=0
for k1 in counts:
p1=float(counts[k1])/total
for k2 in counts:
if k1==k2: continue
p2=float(counts[k2])/total
imp+=p1*p2
return imp
# Entropy is the sum of p(x)log(p(x)) across all
# the different possible results
def entropy(rows):
from math import log
log2=lambda x:log(x)/log(2)
results=uniquecounts(rows)
# Now calculate the entropy
ent=0.0
for r in results.keys():
p=float(results[r])/len(rows)
ent=ent-p*log2(p)
return ent
def printtree(tree,indent=''):
# Is this a leaf node?
if tree.results!=None:
print str(tree.results)
else:
# Print the criteria
print str(tree.col)+':'+str(tree.value)+'? '
# Print the branches
print indent+'T->',
printtree(tree.tb,indent+' ')
print indent+'F->',
printtree(tree.fb,indent+' ')
def getwidth(tree):
if tree.tb==None and tree.fb==None: return 1
return getwidth(tree.tb)+getwidth(tree.fb)
def getdepth(tree):
if tree.tb==None and tree.fb==None: return 0
return max(getdepth(tree.tb),getdepth(tree.fb))+1
from PIL import Image,ImageDraw
def drawtree(tree,jpeg='tree.jpg'):
w=getwidth(tree)*100
h=getdepth(tree)*100+120
img=Image.new('RGB',(w,h),(255,255,255))
draw=ImageDraw.Draw(img)
drawnode(draw,tree,w/2,20)
img.save(jpeg,'JPEG')
def drawnode(draw,tree,x,y):
if tree.results==None:
# Get the width of each branch
w1=getwidth(tree.fb)*100
w2=getwidth(tree.tb)*100
# Determine the total space required by this node
left=x-(w1+w2)/2
right=x+(w1+w2)/2
# Draw the condition string
draw.text((x-20,y-10),str(tree.col)+':'+str(tree.value),(0,0,0))
# Draw links to the branches
draw.line((x,y,left+w1/2,y+100),fill=(255,0,0))
draw.line((x,y,right-w2/2,y+100),fill=(255,0,0))
# Draw the branch nodes
drawnode(draw,tree.fb,left+w1/2,y+100)
drawnode(draw,tree.tb,right-w2/2,y+100)
else:
txt=' \n'.join(['%s:%d'%v for v in tree.results.items()])
draw.text((x-20,y),txt,(0,0,0))
def classify(observation,tree):
if tree.results!=None:
return tree.results
else:
v=observation[tree.col]
branch=None
if isinstance(v,int) or isinstance(v,float):
if v>=tree.value: branch=tree.tb
else: branch=tree.fb
else:
if v==tree.value: branch=tree.tb
else: branch=tree.fb
return classify(observation,branch)
def prune(tree,mingain):
# If the branches aren't leaves, then prune them
if tree.tb.results==None:
prune(tree.tb,mingain)
if tree.fb.results==None:
prune(tree.fb,mingain)
# If both the subbranches are now leaves, see if they
# should merged
if tree.tb.results!=None and tree.fb.results!=None:
# Build a combined dataset
tb,fb=[],[]
for v,c in tree.tb.results.items():
tb+=[[v]]*c
for v,c in tree.fb.results.items():
fb+=[[v]]*c
# Test the reduction in entropy
delta=entropy(tb+fb)-(entropy(tb)+entropy(fb)/2)
if delta>mingain:
# Merge the branches
tree.tb,tree.fb=None,None
tree.results=uniquecounts(tb+fb)
def mdclassify(observation,tree):
if tree.results!=None:
return tree.results
else:
v=observation[tree.col]
if v==None:
tr,fr=mdclassify(observation,tree.tb),mdclassify(observation,tree.fb)
tcount=sum(tr.values())
fcount=sum(fr.values())
tw=float(tcount)/(tcount+fcount)
fw=float(fcount)/(tcount+fcount)
result={}
for k,v in tr.items(): result[k]=v*tw
for k,v in fr.items(): result[k]=v*fw
return result
else:
if isinstance(v,int) or isinstance(v,float):
if v>=tree.value: branch=tree.tb
else: branch=tree.fb
else:
if v==tree.value: branch=tree.tb
else: branch=tree.fb
return mdclassify(observation,branch)
def variance(rows):
if len(rows)==0: return 0
data=[float(row[len(row)-1]) for row in rows]
mean=sum(data)/len(data)
variance=sum([(d-mean)**2 for d in data])/len(data)
return variance
def buildtree(rows,scoref=entropy):
if len(rows)==0: return decisionnode()
current_score=scoref(rows)
# Set up some variables to track the best criteria
best_gain=0.0
best_criteria=None
best_sets=None
column_count=len(rows[0])-1
for col in range(0,column_count):
# Generate the list of different values in
# this column
column_values={}
for row in rows:
column_values[row[col]]=1
# Now try dividing the rows up for each value
# in this column
for value in column_values.keys():
(set1,set2)=divideset(rows,col,value)
# Information gain
p=float(len(set1))/len(rows)
gain=current_score-p*scoref(set1)-(1-p)*scoref(set2)
if gain>best_gain and len(set1)>0 and len(set2)>0:
best_gain=gain
best_criteria=(col,value)
best_sets=(set1,set2)
# Create the sub branches
if best_gain>0:
trueBranch=buildtree(best_sets[0])
falseBranch=buildtree(best_sets[1])
return decisionnode(col=best_criteria[0],value=best_criteria[1],
tb=trueBranch,fb=falseBranch)
else:
return decisionnode(results=uniquecounts(rows))
K-Nearest Neighbors:
This algorithm builds a classifier similar to the ones mentioned before, by taking in a training set of data. However, it classifies data based off of how close its attributes are to the trained model's attributes. The algorithm assigns the input data a class label based off of its relative distance from training data objects. In this algorithm, the input data does not need to match class criteria perfectly in order to be classified.
The following code is an implementation of a K-Nearest Neighbors Classifier in Python for classifying wine:
def wineprice(rating,age):
peak_age=rating-50
# Calculate price based on rating
price=rating/2
if age>peak_age:
# Past its peak, goes bad in 10 years
price=price*(5-(age-peak_age)/2)
else:
# Increases to 5x original value as it
# approaches its peak
price=price*(5*((age+1)/peak_age))
if price<0: price=0
return price
def wineset1():
rows=[]
for i in range(300):
# Create a random age and rating
rating=random()*50+50
age=random()*50
# Get reference price
price=wineprice(rating,age)
# Add some noise
price*=(random()*0.2+0.9)
# Add to the dataset
rows.append({'input':(rating,age),
'result':price})
return rows
def euclidean(v1,v2):
d=0.0
for i in range(len(v1)):
d+=(v1[i]-v2[i])**2
return math.sqrt(d)
def getdistances(data,vec1):
distancelist=[]
# Loop over every item in the dataset
for i in range(len(data)):
vec2=data[i]['input']
# Add the distance and the index
distancelist.append((euclidean(vec1,vec2),i))
# Sort by distance
distancelist.sort()
return distancelist
def knnestimate(data,vec1,k=5):
# Get sorted distances
dlist=getdistances(data,vec1)
avg=0.0
# Take the average of the top k results
for i in range(k):
idx=dlist[i][1]
avg+=data[idx]['result']
avg=avg/k
return avg
def inverseweight(dist,num=1.0,const=0.1):
return num/(dist+const)
def subtractweight(dist,const=1.0):
if dist>const:
return 0
else:
return const-dist
def gaussian(dist,sigma=5.0):
return math.e**(-dist**2/(2*sigma**2))
def weightedknn(data,vec1,k=5,weightf=gaussian):
# Get distances
dlist=getdistances(data,vec1)
avg=0.0
totalweight=0.0
# Get weighted average
for i in range(k):
dist=dlist[i][0]
idx=dlist[i][1]
weight=weightf(dist)
avg+=weight*data[idx]['result']
totalweight+=weight
if totalweight==0: return 0
avg=avg/totalweight
return avg
def dividedata(data,test=0.05):
trainset=[]
testset=[]
for row in data:
if random()>test:
testset.append(row)
else:
trainset.append(row)
return trainset,testset
def testalgorithm(algf,trainset,testset):
error=0.0
for row in testset:
guess=algf(trainset,row['input'])
error+=(row['result']-guess)**2
#print row['result'],guess
#print error/len(testset)
return error/len(testset)
def crossvalidate(algf,data,trials=100,test=0.1):
error=0.0
for i in range(trials):
trainset,testset=dividedata(data,test)
error+=testalgorithm(algf,trainset,testset)
return error/trials
def wineset2():
rows=[]
for i in range(300):
rating=random()*50+50
age=random()*50
aisle=float(randint(1,20))
bottlesize=[375.0,750.0,1500.0][randint(0,2)]
price=wineprice(rating,age)
price*=(bottlesize/750)
price*=(random()*0.2+0.9)
rows.append({'input':(rating,age,aisle,bottlesize),
'result':price})
return rows
def rescale(data,scale):
scaleddata=[]
for row in data:
scaled=[scale[i]*row['input'][i] for i in range(len(scale))]
scaleddata.append({'input':scaled,'result':row['result']})
return scaleddata
def createcostfunction(algf,data):
def costf(scale):
sdata=rescale(data,scale)
return crossvalidate(algf,sdata,trials=20)
return costf
weightdomain=[(0,10)]*4
def wineset3():
rows=wineset1()
for row in rows:
if random()>0.5:
# Wine was bought at a discount store
row['result']*=0.6
return rows
def probguess(data,vec1,low,high,k=5,weightf=gaussian):
dlist=getdistances(data,vec1)
nweight=0.0
tweight=0.0
for i in range(k):
dist=dlist[i][0]
idx=dlist[i][1]
weight=weightf(dist)
v=data[idx]['result']
# Is this point in the range?
if v>=low and v>=high:
nweight+=weight
tweight+=weight
if tweight==0: return 0
# The probability is the weights in the range
# divided by all the weights
return nweight/tweight
from pylab import *
def cumulativegraph(data,vec1,high,k=5,weightf=gaussian):
t1=arange(0.0,high,0.1)
cprob=array([probguess(data,vec1,0,v,k,weightf) for v in t1])
plot(t1,cprob)
show()
def probabilitygraph(data,vec1,high,k=5,weightf=gaussian,ss=5.0):
# Make a range for the prices
t1=arange(0.0,high,0.1)
# Get the probabilities for the entire range
probs=[probguess(data,vec1,v,v+0.1,k,weightf) for v in t1]
# Smooth them by adding the gaussian of the nearby probabilites
smoothed=[]
for i in range(len(probs)):
sv=0.0
for j in range(0,len(probs)):
dist=abs(i-j)*0.1
weight=gaussian(dist,sigma=ss)
sv+=weight*probs[j]
smoothed.append(sv)
smoothed=array(smoothed)
plot(t1,smoothed)
show()
NOTE: The python code was obtained from the book Collective Intelligence written by Toby Segaran. The images were pulled from Wikipedia.