Gambling - Baccarat Chemin de Fer
The goal of this project was to determine if a machine, by blinding making any and all valid moves in a simple game, can come to develop a winning (or at least the best) strategy. The Chemin de Fer style of Baccarat was chosen because it is a relatively simple game that still involves some basic strategic thinking.
The Game - A Primer
Baccarat is a game played amongst two or more players with 6 standard decks. The game can be reduced to a two player game without losing any interesting facets. A player's hand is scored by only considering the least significant digit of their hand's score. Aces are low and all face cards are worth 10 (effectively 0). Suites are irrelevant, only the card's rank matters. In this particular brand of baccarat, there is a player and a banker (the banker is simply another player -- not the house). The banker deals two cards to the player and two to himself. If either player has a score of 8 or 9, the hand ends and the winner is decided (draws are possible). If neither player has an 8 or 9 score, the player may choose to draw a third card. If drawn, the card is placed face up in view of the banker. The banker may then choose to draw a third card. After both players make their decisions, the hand ends and the winner is decided. If and only if the player wins, the banker is rotated to the next player (in our example, the two player's simply switch roles).
Tool Chain
Because of its statistical nature, it made sense to generate hands randomly. This step isn't important. For instance, our hypothetical learning machine could sit at an actual table making random moves and recording the results of the game. What counts is that there are many samples that cover most of the playing space. The actual hands were generated by a C♯ application using a cryptographically-strong random number generator to prevent any bias from weaker generators. The hands were then written out to a csv file and read directly into KNIME for processing.
Sample Generated Hands
| Game | Hand | p1.IsBanker | p1.1 | p1.2 | p1.InitialValue | p1.3? | p1.3 | p1.FinalValue | p2.1 | p2.2 | p2.InitialValue | p2.3? | p2.3 | p2.FinalValue | Outcome |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 5 | 9 | 4 | 1 | 0 | 4 | 6 | 8 | 4 | 0 | 0 | 4 | draw |
| 1 | 2 | 0 | 8 | 1 | 9 | 0 | 0 | 9 | 5 | 0 | 5 | 0 | 0 | 5 | player1 |
| 1 | 3 | 1 | 8 | 7 | 5 | 0 | 0 | 5 | 3 | 0 | 3 | 0 | 0 | 3 | player1 |
| 1 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 7 | 1 | 0 | 0 | 1 | player2 |
Mining
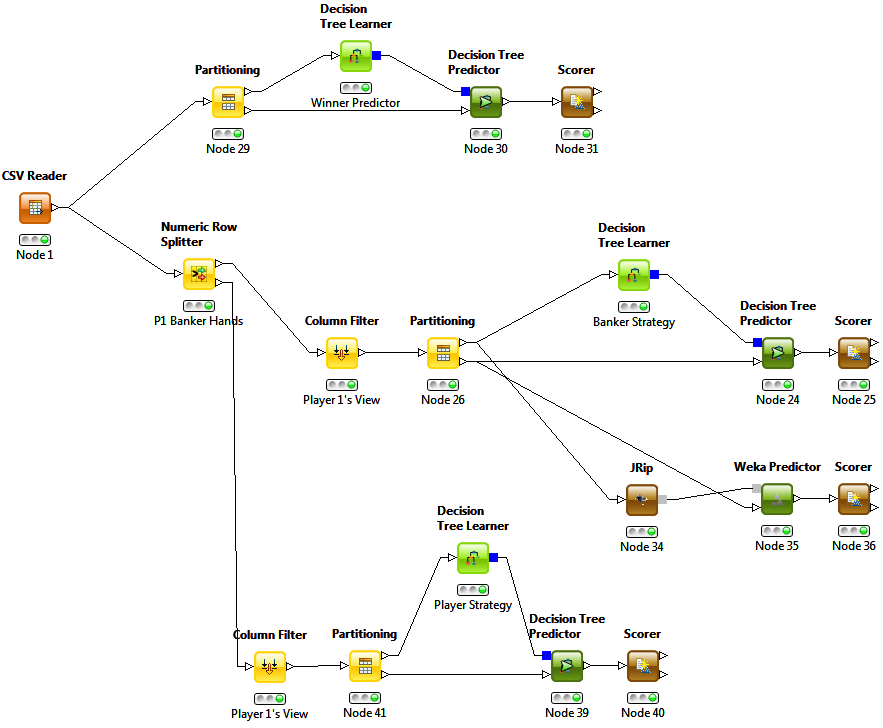
Preprocessing
Because the data is generated, it can be outputted in any format. The particular columns above were picked to represent an exhaustive description of a standard game. Those columns encode all information that could possibly be relevant when deciding on a strategy. The choice to use 0 as a default value for the third card columns when a third card wasn't drawn is important. This allows us to use algorithms that only work with numeric data. 0 was chosen because when a third card isn't drawn, it's as if one was drawn but it was a card with score 0.
KNIME
Once in KNIME, a very simple test was done to make sure the values were within reason. Each player's final score was fed into a decision tree along with the winner class label. The decision tree built by KNIME correctly reasoned that the player with the higher score won and that matching scores were draws. The rest of the analysis was done from Player 1's perspective (an irrelevant choice).
The simpler position to analyze is when Player 1 is the non-banker player. The only information they have available when deciding to draw a third card is their initial 2 card score. This is represented by the bottom branch of the workflow. All records where Player 1 was the Player were split off and only the relevant columns were retained (Player 1's Initial Score, whether or not Player 1 drew a third card, and the outcome of the hand).
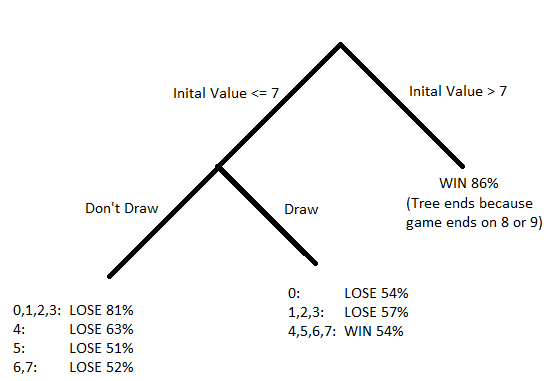
This makes sense given the rules of the game. If the Player gets an 8 or a 9, the game automatically ends that there is no choice to be made (and the player most likely won the hand since the only possible way they could lose is if they had an 8 and the Banker had a nine). Given that the game didn't end and the player needs to make a choice... not drawing would be a bad idea if they have 0-4. If they start with 5, it's almost 50-50 whether drawing a third card will help. This follows the established custom of hitting on 0-4 and making a guess when presented with 5.
The second branch explores the more complicated role of the banker. Not only does the banker have to consider his initial score, but he also must consider whether or not the Player chose to pick another card and what that card's value is.
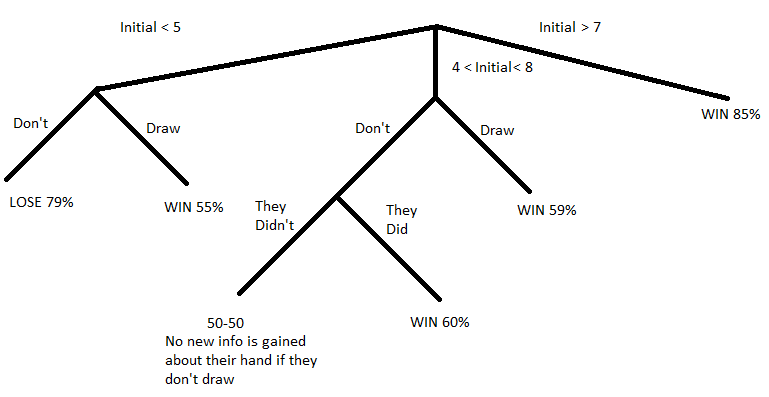
Again, one sees that if the banker draws a 8 or 9, the game ends and they probably won. Also, if they start low and don't draw a third card, they probably will lose. However, if they are is the mid-ranges, it can be seen that nothing changes if the other player doesn't draw. But, if the other player does draw, it is wise to stay and hold the middle ground.
Problems
KNIME
KNIME's built-in data nodes don't deal with conditional attributes very well. A deeper understanding of the game can be gained by explicitly considering the conditional aspect of whether or not a third card was drawn (instead of using the 0 trick for the value of the third card).
Conclusions
This simple example shows that as long as you bother to collect the data, even random moves can be analyzed to improve playing strategy. In this example, the statistically sound, clear cut rules for the player of always staying above 5, hitting below 5, and 50-50 odds at 5 weren't exposed fully; but they were at least partially revealed. Even the correct banker rules were partially revealed. The table below summarizes the statistically sound moves when playing as the banker:
| First two cards total: | Draws when player's third card is: | Stands when player's third card is: |
| 3 | 1-2-3-4-5-6-7-9-10 | 8 |
| 4 | 2-3-4-5-6-7 | 1-8-9-10 |
| 5 | 4-5-6-7 | 1-2-3-8-9-10 |
| 6 | 6-7 | 1-2-3-4-5-8-9-10 |
| 7 | Stands | |
| 8-0 | Natural -- Stands | |
| 0-1-2 | Always draws |
It must me remembered that these rules were deduced from a mere 100 games of completely random play. It would be instructive to re-run these mining procedures on output generated by "experts" that make the correct move 95% of the time. The hypothetical situation for this scenario would be a spectator at a professional tournament that knows nothing about the game. This is as opposed to two players that both know nothing about the game as in our example.