K-Nearest Neighbors

Introduction

K-Nearest Neighbor is a also knowns as lzay learning classifier. Decision tree and rule-based classifiers are designed to learn a model that maps the input attributes to the class lable as soon as the training data becomes available, and thus they are known as eager learning classifiers. Unlike eager learning classifier, K-Nearest Neight do not construct a classification model from data, it performs classification by matching the test instance with K traning examples and decides its class based on the simaliary to K nearest neighbors.

K-Nearest Neightbors Classification Method

The basic idea of K-Nearest Neighbors is best exemplitied by the following saying "If it walks like a duck, quacks like a duck, and looks like a duck, then it's probably a duck." [ 1 ] It explains the idea that the class of a test instance is determined by the class type of its nearest neighbors.

K-Nearest Neighbors classifier represents each example as a data point in a d-dimensional space, where d is the number of attribute. Given a tes example, we compute its proximity to the rest of the data points in the training set, using a appropriate proximity measurement metric. The k-nearest neighbors of a given point z means the k points that are closest to point z. Then the data point z is classified based on the class lables of its neighbors. If the neighbors have more than one lable, the data point is assigned to the majority class of its nearest neighbors.

As shown in the following picture, we want to identify the class lable of a unknown record. In a set of training data, the class lable of other data objects are known. Also the number of K is given before classification. The major steps to perform K-Nearest Neighbors classification are:

Compute the distance from the unknown record to other training records.
Identify k nearest neighbors based on distance metric
Use class lables of nearest neighbors to determine the class lable of unknown record. If there is one class label in the neighbors, then the unknown record is assigned to the same class lable. If the neighbors have more than one class labels, then the class label of unknown record is determined by taking majority vote.

Choosing the value of K

Choosing a proper K value is imprtance to the performance of K-Nearest Neighbor classifier. If k value is too large, as shown in the following figure, the nearest neighbor classifier may misclassify the tes instance because its list of nearest neighbors may include data points that are located far away from its neighborhood. On the other hand, if k value is too small, then the nearest neighbor classifier may be susceptible to iverfitting because of noise in the training data set.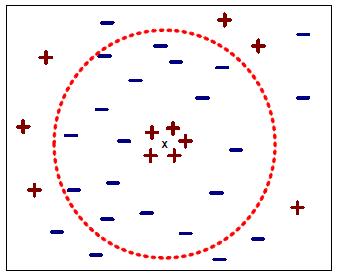

Algorithm

The high-level summary of K-nearest neighbor classification method is formally given as below. [ 1 ] The algorithm computes the distance between each test example and all the training examples to determine its nearest-neighbor list. Such computation can be costly if the number of training exammples is large. However, efficient indexing techniques are available to reduce the amount of computations needed to find the nearest neighbors of a test example. Once the nearest neighbor list is obtained, the test example is classified based on the majority class of its nearest neighbors.

   
	Algorithm: The k-nearest neighbor classification algorithm
    Input: Let k be the number of nearest neighbors and D be the set of training examples.
    for each test example z=(x',y') do
        Compute d(x',x), the distance between z and every example, (x, y) ∈ D
        select D_z in D, the set of k closest training examples to z.
        y'=argmax Σ _{(x_i,y_i) ∈ Dz} I(v=y_i)
    end for

kNN is a relatively simple algorithm to implement. It is computationally intensive, but it does have the advantage of not requiring retraining every time new data is added. Here is an example kNN function [ 2 ]. It uses the list of distances and averages the top k results.

 def knnestimate(data,vec1,k=3):
# Get sorted distances
dlist=getdistances(data,vec1)
avg=0.0
# Take the average of the top k results
for i in range(k):
idx=dlist[i][1]
avg+=data[idx]['result']
avg=avg/k
return avg

def getdistances(data,vec1):
distancelist=[]
for i in range(len(data)):
vec2=data[i]['input']
distancelist.append((euclidean(vec1,vec2),i))
distancelist.sort( )
return distancelist

Conclusion

K-Nearest neighbor classification is a general technique to learn classification based on instance and do not have to develop an abstract model from the training data set. However the classification process could be very expensive because it needs to compute the similiary values individually between the test and training examples. K-nearest neighbor classifer also suffers from the scaling issue. It computes the proximity among the test example and training examples to perform classification. If the attributes have different scales, the proximity distance might be donimated by one of the attributes, which is not good.

References

[1] Introduction to Data Mining, Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Published by Addison Wesley.

[2] Programming Collective Intelligence, Toby Segaran, First Edition, Published by O’ Reilly Media, Inc.