Data Mining Portfolio

Decision Trees

Definition

Decision trees are a classification strategy that traverses a tree of questions depending on the answer of each question until a leaf node is reached, at which point the leaf node states what the input is classified as. Decision trees contain three types of nodes: root node, internal nodes, and leaf nodes. The root node can be considered the entrance to the tree and has no incoming egdes. Internal nodes are all teh nodes have at least one outgoing edge and are found sandwhiched in between the root and leaf nodes. Lastly, the leaf nodes are nodes with no children (outgoing edges) and contain contain a classification. Each non-leaf node has an attribute test condition, which is essentially a question about the input that can split the data into at least two groups. So in order to classify some input one need only traverse the tree from the root to a leaf depending on the result of the attribute test condition. For example using the decision tree below, if there is some input with an attribute A=red and B=10 then the input is classified as x. If, however the value for B of this same input happened to be 0 then by decision tree would have classified the input as y.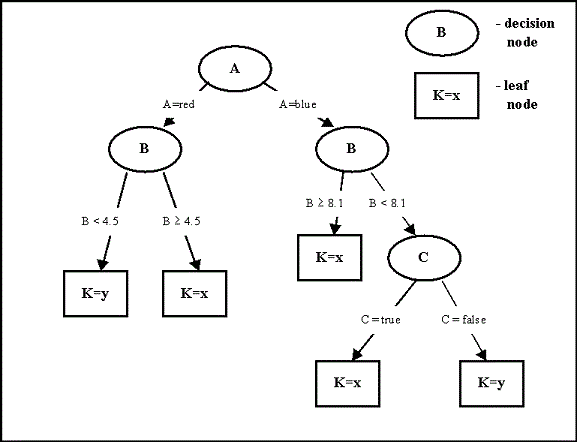

Source: http://dms.irb.hr/tutorial/tut_dtrees.php

Construction

One common construction algorithm for decision trees is known as Hunt's algorithm. Hunt's algorithm grows a decision tree recursively by partitioning a training data set into smaller, purer subsets. This algorithm contains two steps in order to construct a decision tree. The first step, which is the terminating step for the recursive algorithm, checks if every record in a node is of the same class. If so, the node is labeled as a leaf node with its classification the class name of all the records within. If a node is not pure then the second step selects/creates an attribute test condition to partition the data into two purer data sets. From here a child node is created for each subset. The algorithm recurses until the all leaf nodes are found. A common means of deciding which attribute test condition should be used is the notion of the "best split." This concept boils down to choosing the test condition that results in subsets that are purer (where purity is richer when the set contains records of the same class). Three common formulas for calculating impurity is entropy, gini, and classification error.

One interesting aspect of the decision tree classifier is that it is human readable and understood. One need only traverse the tree and test against the test conditions to see how a conclusion/classification was made. This level of transparency is not as prevalent in other classification models like ANN which are almost like a black box. In an ANN the series of weights attached to each connection really contains no inidividual meaning, but each step of the decision tree is clearly understood.